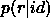 and
and 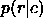 .
XMM position errors were taken to be 2.0 arcsecs.
.
XMM position errors were taken to be 2.0 arcsecs.
The field with the most complete set of data, and the hence the most complete analysis, is the Lockman Hole field.
Fig.reffig:tblo shows differential histograms of 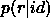 and
and 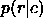 .
XMM position errors were taken to be 2.0 arcsecs.
.
XMM position errors were taken to be 2.0 arcsecs.
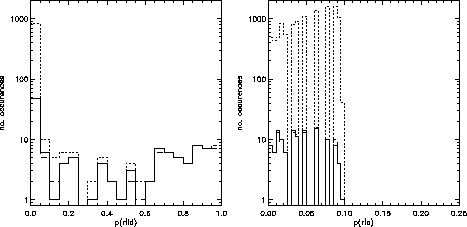
Figure: Histograms of a)  and b)
and b)  for the Lockman Hole field.
Dotted line: all candidates out to 50 arcsecs.
Solid line: most likely candidate for each source.
Dashed line: closest candidate for each source.
for the Lockman Hole field.
Dotted line: all candidates out to 50 arcsecs.
Solid line: most likely candidate for each source.
Dashed line: closest candidate for each source.
The `binning' effect in Fig.reffig:tblo(b) is due to the finite width of the magnitude bins in the background density calculation.
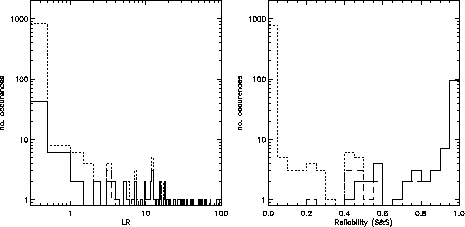
Figure: Histograms of a) likelihood ratio and b) reliability for the
Lockman Hole field.
Dotted line: all candidates out to 50 arcsecs.
Solid line: most likely candidate for each source.
Dashed line: closest candidate for each source.
Restricting the optical catalogue to objects brighter than a certain limit (say M=20) removes a large fraction of the candidates with low likelihood ratio as expected.
Although in most cases (116 out of 121 sources) the closest object is the most
likely, explaining why the solid and dashed curves mostly coincide in figures
![]() and
and ![]() , the discrepancy is more apparent in the
reliability histogram, which put an emphasis on the fact that there are more
than one candidate per source. Fig.
, the discrepancy is more apparent in the
reliability histogram, which put an emphasis on the fact that there are more
than one candidate per source. Fig. ![]() shows the difference
between the two methods of calculating reliability outlined in
section
shows the difference
between the two methods of calculating reliability outlined in
section ![]() . Which method should we choose? At the moment we are
using the Sutherland & Saunders method but the other gives more contrasted
results.
. Which method should we choose? At the moment we are
using the Sutherland & Saunders method but the other gives more contrasted
results.
In this case the identification fraction with a search radius of 5 arcsecs was
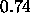 . Tables of all XMM sources in this field with corresponding WFC matches
and the likelihood ratio and reliability for these associations
can be found here:
. Tables of all XMM sources in this field with corresponding WFC matches
and the likelihood ratio and reliability for these associations
can be found here:
http://www.ast.cam.ac.uk/ xmmssc/internal/lockman-hole/
lockman--hole/gh/html/
xmmssc/internal/lockman-hole/
lockman--hole/gh/html/
This page also contains links to colour--colour and flux--magnitude plots for the matched objects and more control plots.
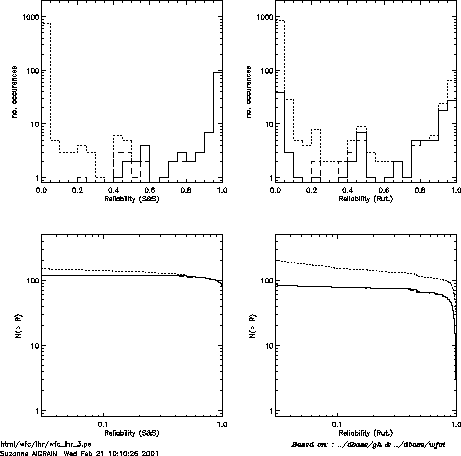
Figure: Histograms of reliability comparing the Sutherland & Saunders (S&S) and Rutledge et al. (Rut.) methods: (a) & (b) differential, (c) & (d) cumulative.