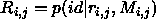Reliability is usually meant as the probability that the true identification
is the candidate being considered [3,6,9],
i.e.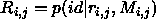 
, and this is the definition we will take.
The simplest estimate for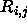 
is [3]:
from Bayes' theorem.
To calculate this quantity in the first instance we will assume 
,
and later work will aim to improve this first estimate in ways outlined in
section 
.
However, the above expression ignores any information about the fact
that there may be more that one candidate for a given source, which is the
case for all XMM sources due to the depth of the optical data. To overcome
this limitation, Sutherland & Saunders [6] derive an alternative
expression, which we will call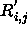 
:
(note this expression differs from that in the Sutherland and Saunders paper because we have opted for a different definition of likelyhood ratio.)
Another way to take into account the possibility of multiple candidates is proposed by Rutledge et al. [9]. The reliability they define is purely a function of the likelihood ratio of the candidate under consideration (and hence does not reflect the eventuality that another candidate may have a similar or higher likelihood ratio). However they go on to evaluate the probability that the candidate is the emphunique identification for the source , and the probability that there is no identification at all, in a separate step, leading to the expressions below.
The probability that there is no identification at all for the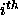 
source
is given by:
where S is a normaisation factor such that
.
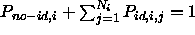We have carried out the calculation for both methods and it appears that the
second one gives more contrasted results, while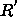 
is nearly always
very close to one for the closest or most likely match.
