



Next: References
Up: No Title
Previous: Results for merged
As seen above, in a small but significant number of cases the closest object
is not the most likely. The quality of the matching would therefore be
improved by taking likelihood ratio and Reliability into account in deciding
which candidate is the true identification, rather than crudely taking the
closest. It also allows us to make fuller use of the information available, as
the magnitude of the candidates is also considered.
The likelihood ratios and reliabilities should be calculated for all
candidates within 15 arcsecs of an XMM sources (this proves sufficient to
detect all best matches over the 9 fields available so far).
Before carrying this out, however, further investigation is needed into the following:
- The influence of position errors in the XMM data has not yet been
investigated (position errors were set to 2.0 arcsecs to obtain the results
presented above). In the case where individual errors are available for each
source, these should be included. In the case where one error value is assigned
to he entire sample, one could vary this value to assess its impact on the
likelihood ratios.
- A better estimate of Q or
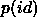 is needed to compute the
reliabilities, as we have simply been setting it to 1 so far, be it with the
Sutherland & Saunders method or with the Rutledge et al. method. The
iterative method employed by Benn [3] to estimate Q has been
described in section
is needed to compute the
reliabilities, as we have simply been setting it to 1 so far, be it with the
Sutherland & Saunders method or with the Rutledge et al. method. The
iterative method employed by Benn [3] to estimate Q has been
described in section  , and a similar calculation could be carried
out in this case.
, and a similar calculation could be carried
out in this case.
The effect of possible offsets in the X--ray positions, or of confusion, can
be important (as outlined by Hogg 2000 [8]).
A technique similar to that employed by Rutledge et al. [9] to
determine the relationship between likelihood ratio and reliability
could be used to calculate reliabilities from the likelyhood ratios without
having to guess a value for 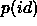 .
For each source field in the optical data, Rutledge et al.
define a number of background fields which are circles of diameter 75 arcsecs
offset from the centre of the source field by varying amounts to the east and
west. The X--ray sources are then matched to optical sources in each field, and
this is used to determine the effective relationship between reliability and
likelihood ratio, which they then use to calculate the probability that a
candidate is the unique identification for a given source
(see section
.
For each source field in the optical data, Rutledge et al.
define a number of background fields which are circles of diameter 75 arcsecs
offset from the centre of the source field by varying amounts to the east and
west. The X--ray sources are then matched to optical sources in each field, and
this is used to determine the effective relationship between reliability and
likelihood ratio, which they then use to calculate the probability that a
candidate is the unique identification for a given source
(see section  ).
).
Similarly, we propose to generate a set of simulated random background optical
objects for a region of a given size, to a certain magnitude limit, with a
power law density.
A set of X--ray sources can be separately generated for the same region
together with the magnitude of their optical counterparts. The X--ray source
positions are then shifted by a small offset which is a function of the r.m.s.
error in the X--ray positions, to simulate confusion.
We would then have generated optical data for a 'source' field (using the true
X--ray positions and the optical magnitudes of their counterparts) and for
background fields, as well as shifted X--ray data for the same field.
Performing
the likelihood ratio calculation on these data will allow us to test the
ability of this technique to pick out confusion effects and, perhaps, will
identify a given method for choosing 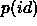 as more suitable than another.
as more suitable than another.




Next: References
Up: No Title
Previous: Results for merged
Richard McMahon
Tue Feb 27 19:44:29 GMT 2001
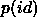 is needed to compute the
reliabilities, as we have simply been setting it to 1 so far, be it with the
Sutherland & Saunders method or with the Rutledge et al. method. The
iterative method employed by Benn [3] to estimate Q has been
described in section
is needed to compute the
reliabilities, as we have simply been setting it to 1 so far, be it with the
Sutherland & Saunders method or with the Rutledge et al. method. The
iterative method employed by Benn [3] to estimate Q has been
described in section 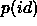 .
For each source field in the optical data, Rutledge et al.
define a number of background fields which are circles of diameter 75 arcsecs
offset from the centre of the source field by varying amounts to the east and
west. The X--ray sources are then matched to optical sources in each field, and
this is used to determine the effective relationship between reliability and
likelihood ratio, which they then use to calculate the probability that a
candidate is the unique identification for a given source
(see section
.
For each source field in the optical data, Rutledge et al.
define a number of background fields which are circles of diameter 75 arcsecs
offset from the centre of the source field by varying amounts to the east and
west. The X--ray sources are then matched to optical sources in each field, and
this is used to determine the effective relationship between reliability and
likelihood ratio, which they then use to calculate the probability that a
candidate is the unique identification for a given source
(see section 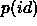 as more suitable than another.
as more suitable than another.