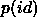 is required to estimate the reliability
is required to estimate the reliability 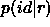 .
In this section we present some
methods used by the authors who chose to include Q in the expression
for the likelyhood ratio.
.
In this section we present some
methods used by the authors who chose to include Q in the expression
for the likelyhood ratio.
Chosing a value for the prior Q is necessary at some point in the
process of evaluating the identifications. Even using equation refeq:lhr,
the value of 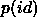 is required to estimate the reliability
is required to estimate the reliability 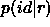 .
In this section we present some
methods used by the authors who chose to include Q in the expression
for the likelyhood ratio.
.
In this section we present some
methods used by the authors who chose to include Q in the expression
for the likelyhood ratio.
Benn [3] uses an iterative method to obtain an estimate for Q, based on the fact that

such that
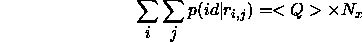
Having calculated the left--hand side of the above from
equations ![]() and
and ![]() , Benn iterates over non--zero
values of Q until both sides converge.
Estimating Q through iteration is one method we may investigate in the
future.
, Benn iterates over non--zero
values of Q until both sides converge.
Estimating Q through iteration is one method we may investigate in the
future.
Wolstencroft et al. [5] have put forward a method for estimating
Q which is quite different.
They take 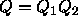 , where
, where 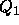 is the
overall probability that an identification exists for the ensemble of all
sources in the sample, and
is the
overall probability that an identification exists for the ensemble of all
sources in the sample, and 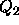 is defined to account for the fact that a
bright candidate is more likely to be the true identification than a fainter
one:
is defined to account for the fact that a
bright candidate is more likely to be the true identification than a fainter
one:
where 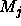 is the magnitude of the
is the magnitude of the 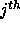 candidate,
candidate, 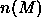 is the number
of candidates with magnitude in the range M to M+dM, and
is the number
of candidates with magnitude in the range M to M+dM, and 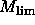 is the
plate limit of the optical sample.
is the
plate limit of the optical sample.
We have preferred to include information on the magnitude of the candidate
only in the value taken for 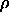 , the background density, as in
Rutledge et al. 2000 [9].
, the background density, as in
Rutledge et al. 2000 [9].