Astrometric Calibration
Field Distortion
Optical systems, particularly those involving refractive elements, do not
have a uniform plate scale over the field and generally have a radial
distortion term which takes the form
r_true = k1 * r + k3 * r**3 + k5 * r **5
where r_true is an idealised angular distance from the optical axis and
r is the measured distance.
Prime focus at the INT is no exception and the ING observer
handbook, page 83, lists the distortion terms for INT PF as k1 = 24.7
arcsec/mm and k3 = -9.202E-05 arcsec/mm**3. These convert measured
distance in mm to true angular distance in arcsec. The term due to k5
is negligible. Rearranging the above equation to a more convenient
form gives
r_true = r' * (1 + k3/k1**3 * r'**2)
where r' is the measured distance from the optical axis in arcsec
using the k1 scale. The default coefficient k3/k1**3 in these units
is -7.59E-09 arcsec**-3. If we convert all units from arcsec to
radians, the default coefficient becomes 259.8, though more recent
measurements of the INT PF distortion using a mixture of photographic
plates and the INT WFC show that a value of 220.0 is more appropriate.
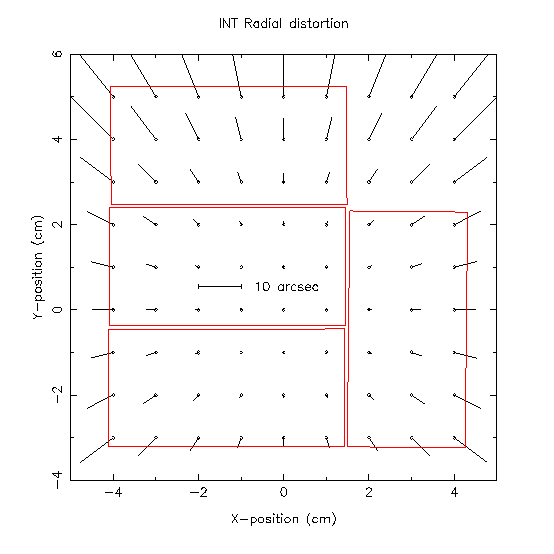
The non-linear term in the above introduces a (pincushion/barrel)
distortion amounting to a differential effect up to 10 arcsec from one
corner of a CCD to the other near the field edges (no vignetting to
r=40 arcmin, 50% vignetting at r=52 arcmin) as illustrated in the
above figure.
Astrometric Accuracy
The end product of the full pipeline currently has an astrometric
precision better than 100mas over the whole array (ie. across CCDs),
as determined by analysis of independently calibrated adjacent
overlapping pointings. Note, however, that this is not the same as
the external accuracy of the FK5 reference frame we are generating,
which is wholly determined by the external accuracy of the reference
frame of the Schmidt plate-based astrometric catalogues. This is
currently limited to about 0.25 arcsec.
By stacking the astrometric residuals from a series of independent pointings
and CCD WCS solutions it is possible to assess the accuracy of the simple
INT distortion model. This is illustrated in the diagram below using the
average residuals from a stack of a one week WFS run.
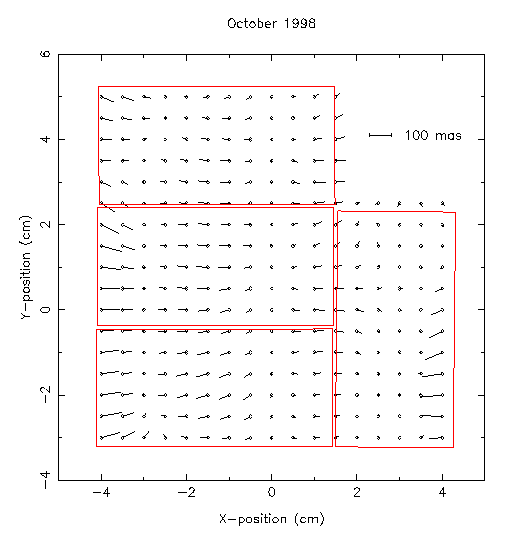
To generate this figure the independent CCD frames were analysed using a
standard linear 6 plate constant model, assuming a fixed optical axis and the
r**3 term outlined above. This pattern appears to be fairly stable over long
periods of time and will form the basis for further astrometric performance
improvements.
Virtual Pixel Mosaic
The individual CCDs making up the mosaic are mechanically rigid since
their CCD carriers are bolted to the baseplate. Therefore unless
the individual CCDs are physically disturbed (unlikely unless severe
problems) their active surfaces should retain a fixed geometric relationship
as shown in the diagram below.
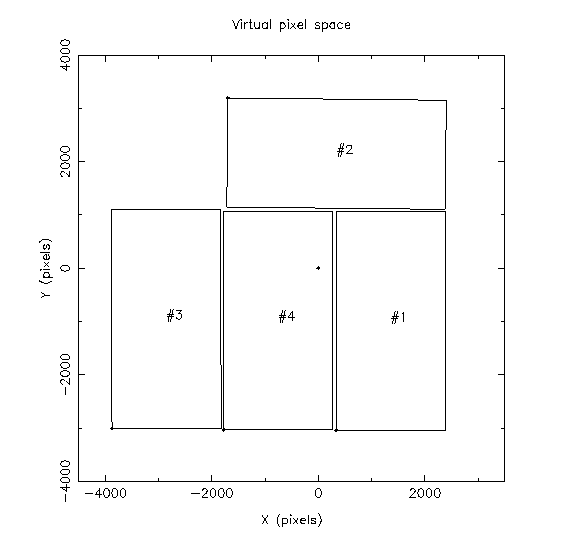
The dot at (0,0) denotes the position of the rotator centre. Apart from
translating the entire system to be centred on the optical axis, all
CCDs have been mapped onto the CCD#4 coordinate system. The blodges in the
CCD corners are the pixels (1,1) for the active part of each CCD, ie. overscan
and underscan trimmed off.
The following relations transform all the CCDs to the CCD#4 pixel system.
Virtual transform constants: (from a set of 30 pointings in ELAIS region)
0.10000E+01 -0.10013E-02 2113.94
0.58901E-03 0.10001E+01 -12.67
Location of rotator centre in CCD-space 1 -332.881 3041.61
-0.10272E-01 0.99992E+00 78.84
-0.10003E+01 -0.10663E-01 6226.05
Location of rotator centre in CCD-space 2 3177.58 1731.94
0.10003E+01 -0.23903E-02 -2096.52
0.24865E-02 0.10003E+01 21.93
Location of rotator centre in CCD-space 3 3880.40 2996.45
0.10000E+01 0.00000E+00 0.00
0.00000E+00 0.10000E+01 0.00
Location of rotator centre in CCD-space 4 1778.00 3029.00
The transforms are in the form
a b c
d e f
and based on CCD#4 pixel system
So to convert a CCD to the CCD#4 system take the pixel location (x,y) on the
CCD and apply the following transformation to it
x' = a*x + b*y + c
y' = d*x + e*y + f
to get to rotator centre replace c -> c-1778
f -> f-3029
Note that the astrometric solution errors for a single 4 chip
solution are about the few parts in 10,000 level and for 30 pointings
about the several parts in 100,000 hence the slightly different scales
etc... These will be updated and improved as we fold in more WCS
solutions.
World Coordinate Systems and FITS Headers
Unfortunately there are several conflicting ways of defining a
World Coordinate System (WCS) for telescopes with focal stations
requiring a general radial distortion model. As yet the FITS
community has not adpoted an agreed final standard. However, much of
the transformation representation has been agreed and there are a
couple of popular, but mutually incompatible, interim solutions
outlined below (see also the WFS cookbook here ).
IRAF uses the following header items to define a WCS transformation
including radial distortion terms
CTYPE1 = 'RA---ZPX' / Type of coordinate on axis 1
CTYPE2 = 'DEC--ZPX' / Type of coordinate on axis 2
CRPIX1 = 3914.68291287068 / Reference pixel on axis 1
CRPIX2 = 2958.23149413302 / Reference pixel on axis 2
CRVAL1 = 325.5563 / Value at ref. pixel on axis 1
CRVAL2 = 0.2084674 / Value at ref. pixel on axis 2
CD1_1 = -1.4011089128826E-6 / Transformation matrix
CD1_2 = -9.2625825594913E-5 / Transformation matrix
CD2_1 = -9.2750922381494E-5 / Transformation matrix
CD2_2 = 1.31362241659925E-6 / Transformation matrix
WAT1_001= 'wtype=zpx axtype=ra projp1=1.0 projp3=220.0'
WAT2_001= 'wtype=zpx axtype=dec projp1=1.0 projp3=220.0'
Several other image processing packages or display programs
(eg. SAOTNG, GAIA) use a similar, but incompatible with IRAF version
and vice-versa, with the following changes,
CTYPE1 = 'RA---ZPN' / Zenithal polynomial projection
CTYPE2 = 'DEC--ZPN' / Zenithal polynomial projection
PROJP1 = 1.0 / coefficient for r term
PROJP3 = 220.0 / coefficient for r**3 term
Note that the ZPX and ZPN projections can be set to give same results.
A possible future WCS style for this type of projection in FITS is
CTYPE1 = 'RA---TAN' / Change projection to TAN
CTYPE2 = 'DEC--TAN' / Change projection to TAN
PV1_11 = 220.0 / split PROJP3 into x and y (PROJP1 assumed
PV2_11 = 220.0 / to be 1.0) note new improved radial terms
/ also allow for generalised polynomial
CRDER1 = 0.4733928 / random error in axis1
CRDER2 = 1.0012080 / random error in axis2
CSYER1 = 0.5 / systematic error in axis1
CSYER2 = 0.5 / systematic error in axis2
But we were wrong and in fact after much debate an agreed form for
the WCS for assorted projections of interest was mooted last Autumn.
Here's an example of what the INT WFC WCS will look like shortly (as
soon as the display and analysis software catches up). For more
details see:
Calabretta & Greisen 2002 A&A 395 1077
Greisen & Calabretta 2002 A&A 395 1061
CTYPE1 = 'RA---ZPN' / Zenithal polynomial projection
CTYPE2 = 'DEC--ZPN' / Zenithal polynomial projection
CRPIX1 = 3914.68291287068 / Reference pixel on axis 1
CRPIX2 = 2958.23149413302 / Reference pixel on axis 2
CRVAL1 = 325.5563 / Value at ref. pixel on axis 1
CRVAL2 = 0.2084674 / Value at ref. pixel on axis 2
CD1_1 = -1.4011089128826E-6 / Transformation matrix
CD1_2 = -9.2625825594913E-5 / Transformation matrix
CD2_1 = -9.2750922381494E-5 / Transformation matrix
CD2_2 = 1.31362241659925E-6 / Transformation matrix
PV2_1 = 1.0 / coefficient for r term
PV2_3 = 220.0 / coefficient for r**3 term
PS. If you are having problems with DS9 version 2.2 or 2.3b
reading ZPN projections don't blame us. Get the latest wcstools patch
and rebuild DS9 sans PV matrix bug. Then make the headers look like
above instead of currently supplied WFC wcs style. DS9 version 2.1
reads the older style currently supplied ok.



