SV93 biconical wind prescription

In the SV93 prescription, the wind emerges between \(r_{min}\) and \(r_{rmax}\) along streamlines whose orientation with respect to the system are described an angle

\[\theta = \theta_{min} + (\theta_{max} - \theta_{min}) x^{\gamma}\]

where

\[x=\frac{r_o - r_{min}}{r_{max}-r_{min}}\]

and \(r_o\) refers to the footpoint of a streamline.

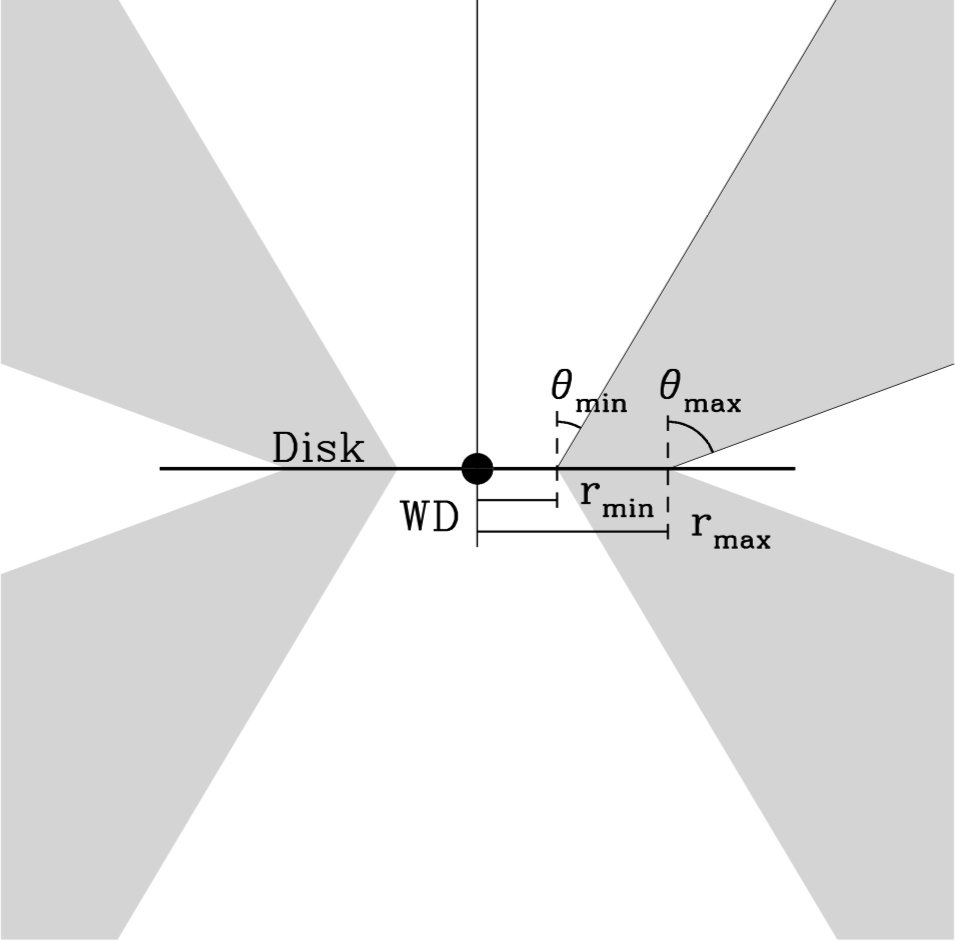
The geometry of a Shlosman & Vitello wind

The poloidal velocity along the streamlines is defined to be

\[v_l - v_o + (v_{\infty}(r_o)-v_o) \frac {(l/R_v)^{\alpha}}{(l/R_v)^{\alpha}+1}\]

The scale length \(R_v\) and the exponent \(\alpha\) control the acceleration of the wind between a velocity \(v_o\), at the base of the wind and the terminal velocity \(v_{\infty}(r_o)\). The initial velocity \(v_o\) can be set to either a constant, normally 6 km/s, or a multiple of the sound-speed at the streamline base. The terminal velocity of each streamline varies depending on the location of the streamline in the inner and outer disk, being characterized as a fixed multiple of the escape velocity at the footpoint of the streamline. Thus the poloidal velocity is greatest for stream lines that originate from the inner regions of the disk, since the gravitational potential that must be overcome is greatest there.

The mass loss per unit surface area \(\delta \dot{m}/\delta A\) of the disk is controlled by a parameter \(\lambda\) such that

\[\frac{\delta\dot{m}}{\delta A} \propto \dot{m}_{wind} r_o^{\lambda} cos(\theta(r_o))\]

With this prescription, the overall mass loss rate declines with radius if \(\lambda\) is somewhat less than -2.

To use the SV93 prescription, therefore, one must provide the basic parameters of the system, the mass of the WD, the accretion rate, the inner and outer radius of the disk, and in addition, for the wind \(\dot{m}_{wind}\), \(r_{min}\), \(r_{max}\), \(\theta_{min}\), \(\theta_{max}\), \(\gamma\), \(R_{\nu}\), \(\alpha\), \(\lambda\), and the multiple of the escape velocity to be used for \(v_{\infty}\).

The following variables are used:

Wind.mdot(msol/yr)                         1e-9
SV.diskmin(units_of_rstar)                 4
SV.diskmax(units_of_rstar)                 12
SV.thetamin(deg)                           20
SV.thetamax(deg)                           65
SV.mdot_r_exponent                         0
SV.v_infinity(in_units_of_vescape          3
SV.acceleration_length(cm)                 7e10
SV.acceleration_exponent                   1.5
SV.v_zero_mode(fixed,sound_speed)                  fixed
SV.v_zero(cm/s)                                                6e5