KWD biconical wind prescription

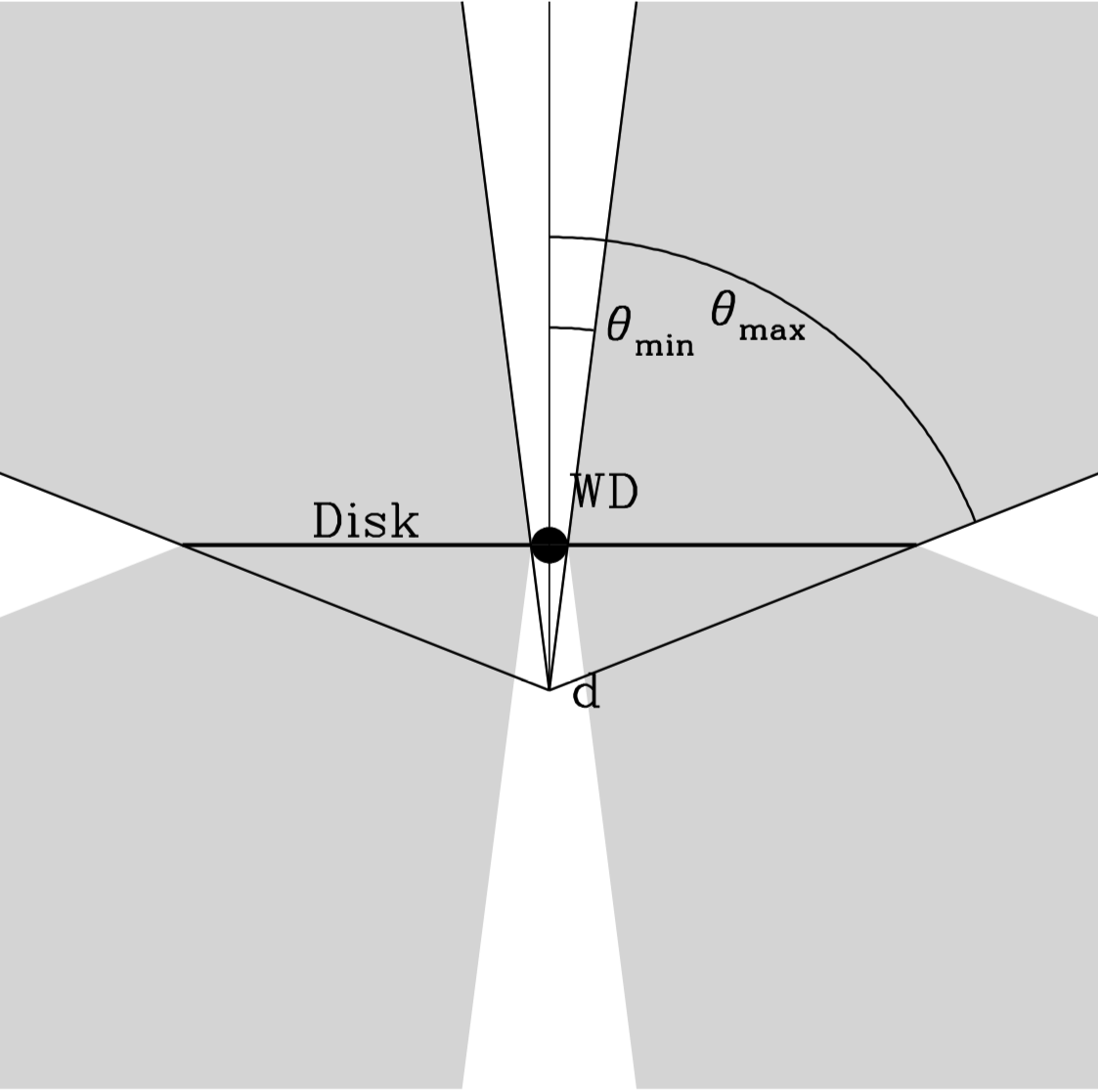
Knigge, Woods & Drew (1995) developed a parameterization for a bi-conical flow, which in slightly modified form is built into Python. in this parameterization, the wind is envisioned to have poloidal streamlines that all point to a position a distance d below the disk, as is shown below:

Todo

This figure needs modification to account for the fact that we allow rmin and rmax to be specified.

../_images/kwd.png

As descried by KWD95, streamlines emerge thoughout the entire disk, with the innermost streamline just grazing the surface of the central object and the outermost streamline emerging from the outer radius of the disk. In the current version of Python, while this is the default choice, the wind region can be restricted to streamlines that arise from between \(r_{min}\) and \(r_{rmax}\). For fixed values of \(r_{min}\) and \(r_{rmax}\), the wind will tend to be more collimated the larger the value of d.

In the KWD parameritization, the mass loss per unit area per unit area of the disk is given by

\[\frac{\delta \dot{m}}{\delta A} \propto T(R)^{4\alpha}\]

where T(R) is the temperature of the disk at radius R. With this parameterization, the mass loss rate per unit area is constant for \(\alpha=0\) and is porportional to the luminoous flux is \(\alpha=1\).

The KWD95 model incorporates a velocity law reminiscent of a stellar wing, viz.

\[v_l=(nc_{s}) + (v_{\infty} - nc_{s})\left(1- \frac{R_{v}}{l+R_{v}} \right)^{\beta}\]

where \(nc_s\) is the speed at the base of flow,a multiple of the sound speed, \(R_v\) is the scale length, \(beta\) is the exponent that determines the number of scale lengths over which the wind acclerates, and \(v_{\infty}\) is defined as a multiple of the escape velocity at the footpoint of each stream line.

For the model, the sound speed of the disk is defined to be

\[c_s(R) = 10 \sqrt{\frac{T_{eff}(R)}{10^4 K}} km s^{-1}\]

The variables that must be defined are as follows:

Wind.mdot(msol/yr)        1e-9
KWD.d(in_units_of_rstar)        16.0
KWD.mdot_r_exponent        1.0
KWD.v_infinity(in_units_of_vescape)        3.0
KWD.acceleration_length(cm)        10000000000.0
KWD.acceleration_exponent                       1.5
KWD.v_zero(multiple_of_sound_speed_at_base)                    1
KWD.rmin(in_units_of_rstar)                       1
KWD.rmax(in_units_of_rstar)                 55.6329