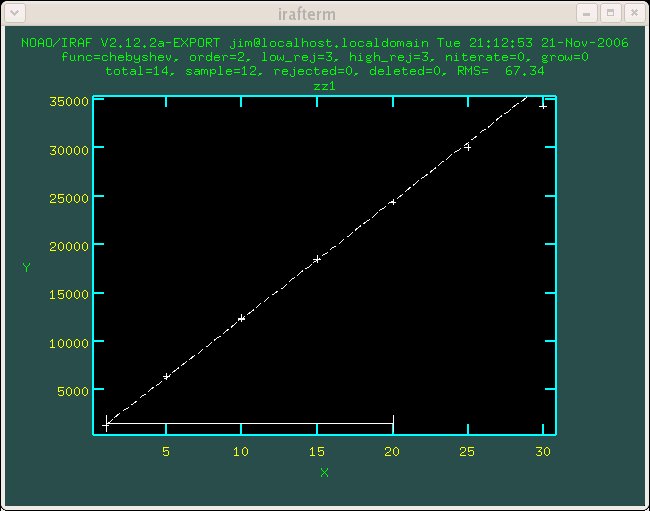
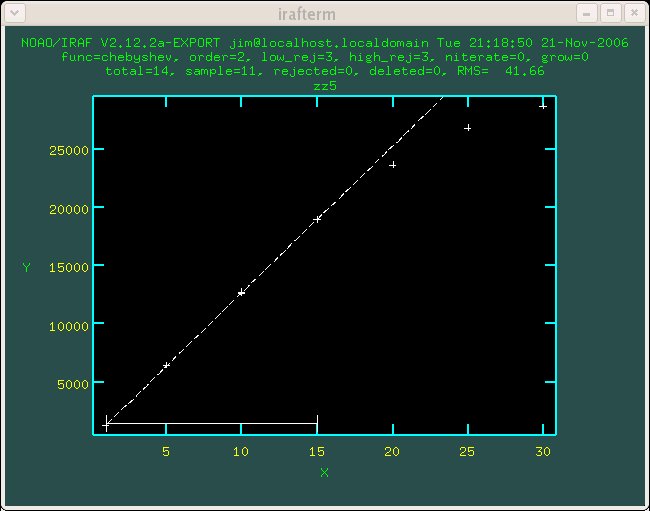
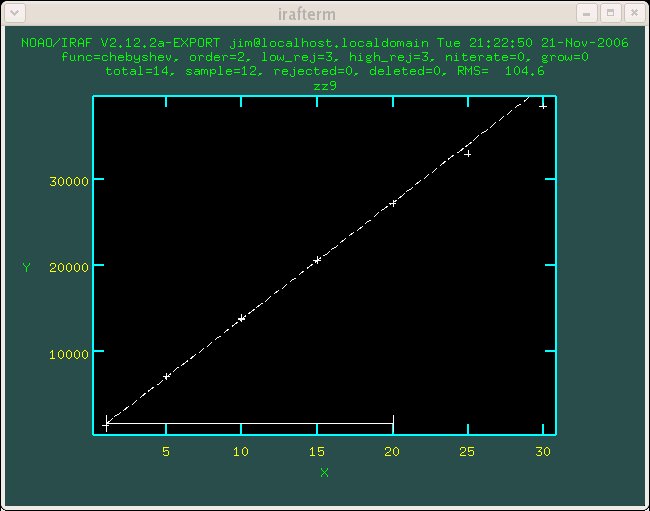
Figure 1.1 Detector 1

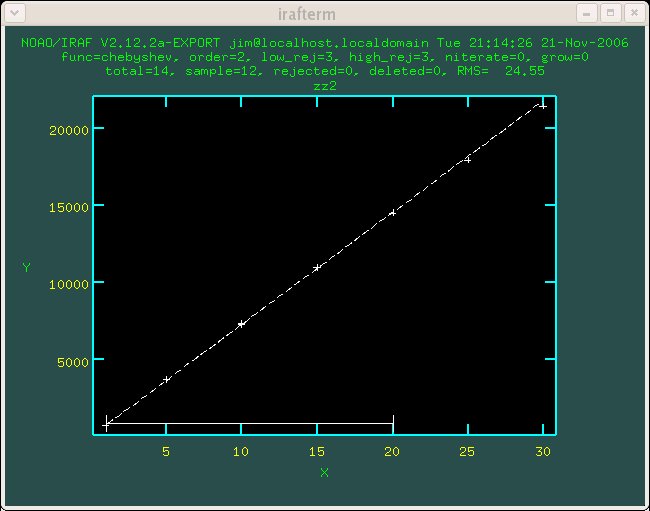
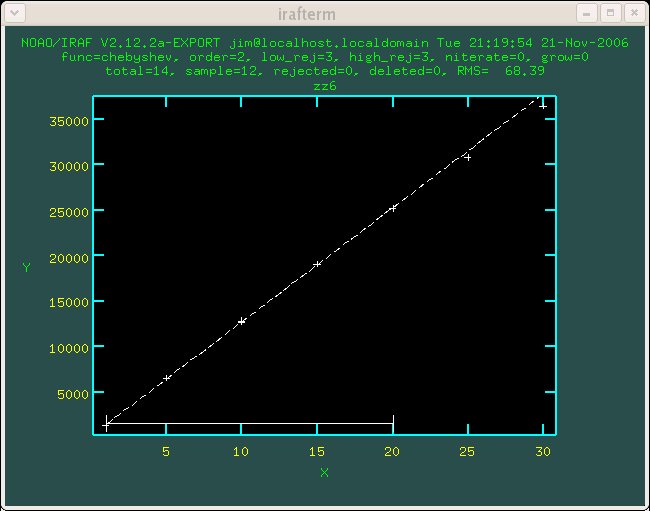
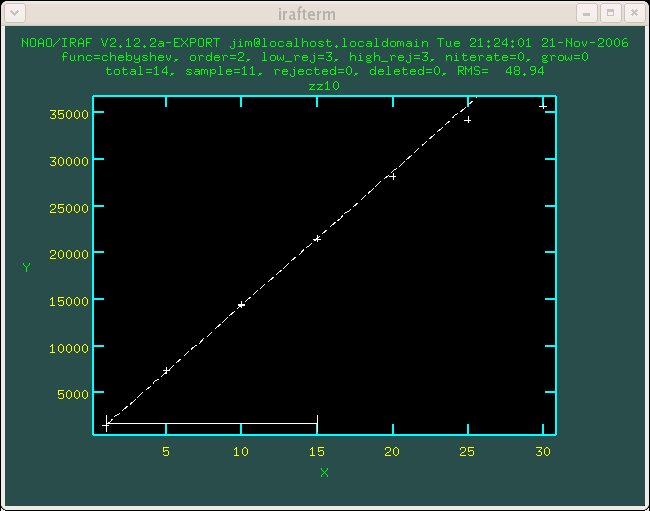
Figure 1.2 Detector 2

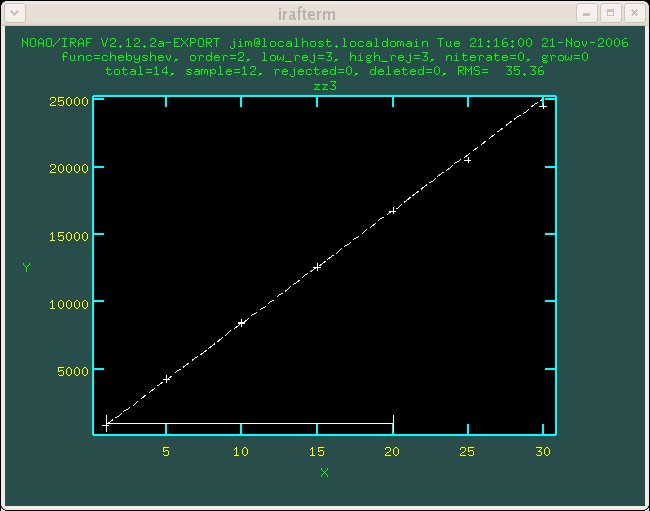
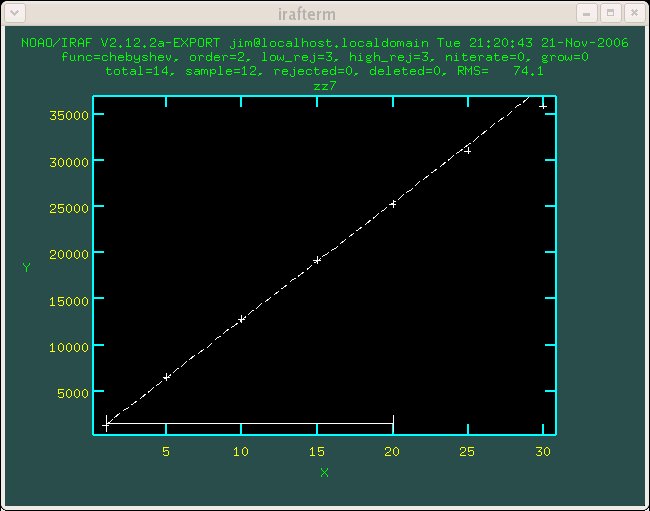
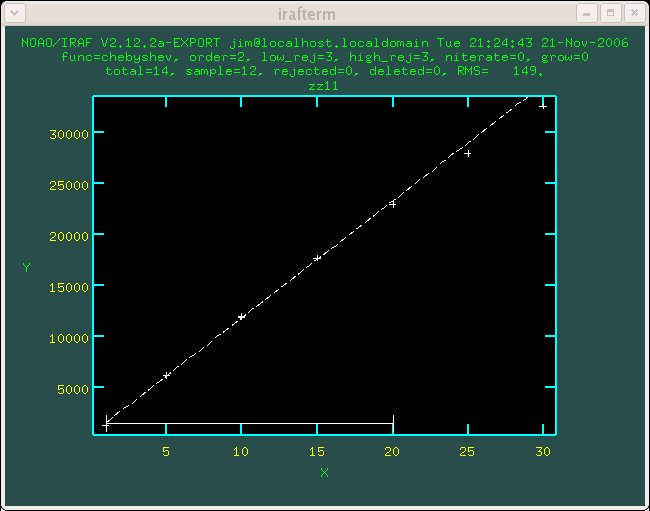
Figure 1.3 Detector 3

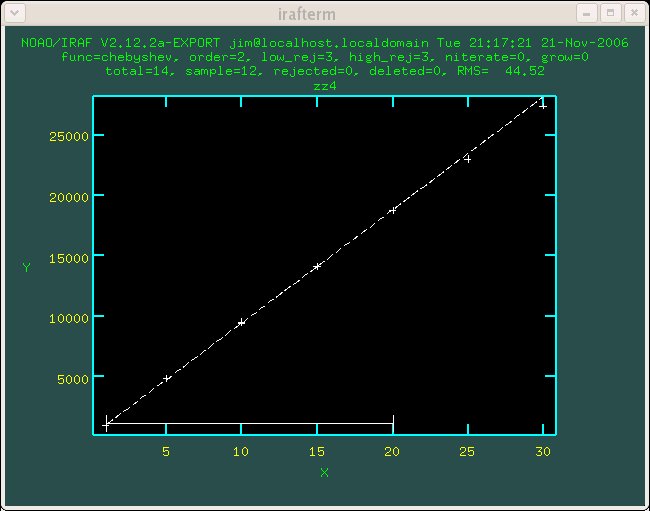
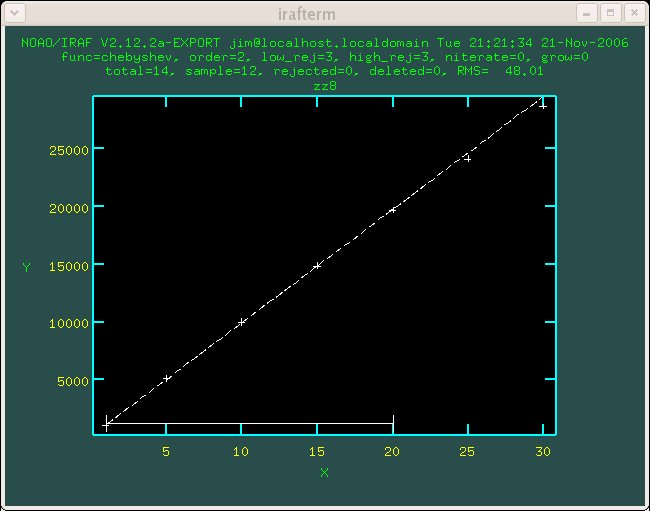
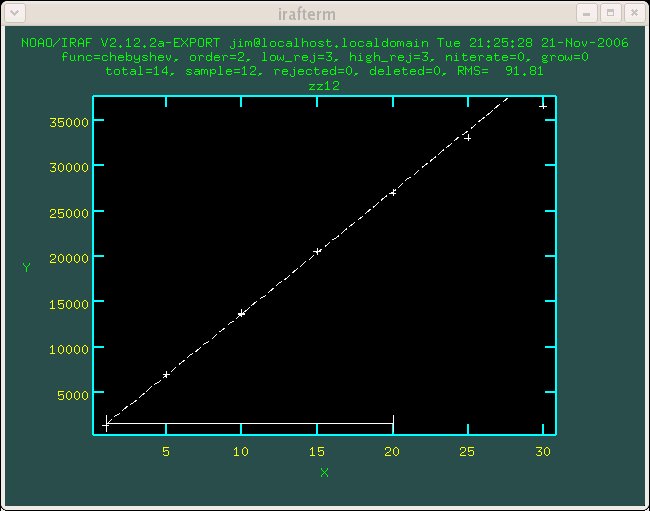
Figure 1.4 Detector 4

Figure 1.5 Detector 5

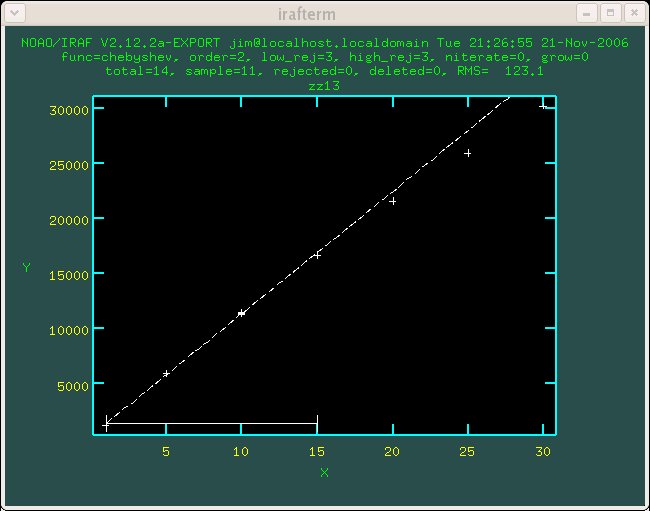
Figure 1.6 Detector 6

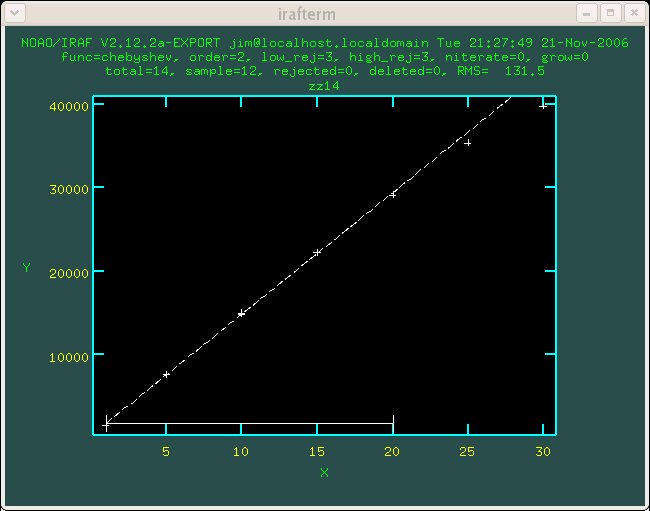
Figure 1.7 Detector 7

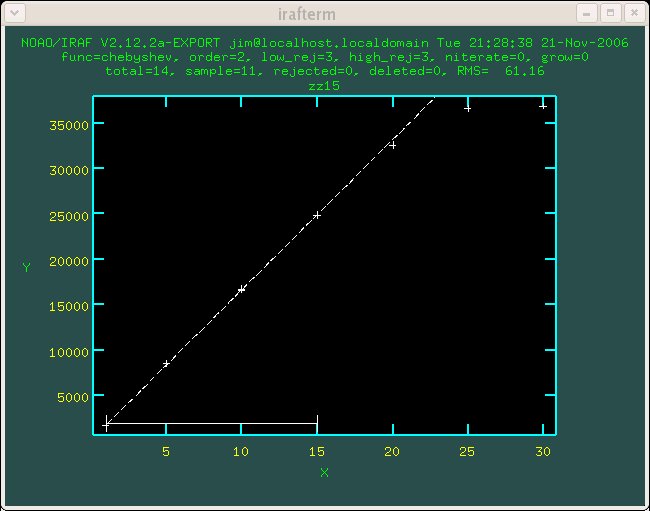
Figure 1.8 Detector 8

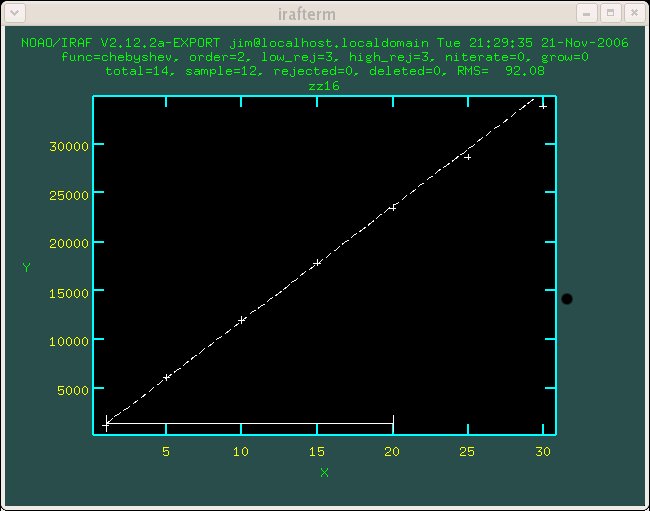
Figure 1.9 Detector 9

Figure 1.10 Detector 10

Figure 1.11 Detector 11

Figure 1.12 Detector 12

Figure 1.13 Detector 13
Figure 1.14 Detector 14
Figure 1.15 Detector 15

Figure 1.16 Detector 16